数据量单位
位(bit)是计算机中最小的存储单位,每一个位可以存储一个二进制码值的 0 或 1。
字节(byte)则通常是由八个位组成的一个存储单元。在计算机中,字节是最小的可寻址单位,这意味着 CPU 在使用数据时,可以以字节为单位,为每一字节内存分配一个相应的独立地址。
字的大小并不固定,一个字的大小可能是 2 的幂次个位,比如 16 位、32 位,也有可能是 12 位、27 位等一些并不常见的大小。而这主要是因为字的概念与具体的处理器或硬件体系架构直接相关,它跟位、字节这种较为通用和统一的数据量概念并不相同。
字是处理器设计时使用的自然数据单位,通常,这个大小会反映在计算机结构和相关操作的多个方面中。比如,处理器中大多数寄存器的容量是与字同样大小的,处理器单个指令可以操作的最大内存块一般为一个字大小,而用于指定内存中某个具体位置的地址,一般也是以处理器的自然字为宽度的。
汇编语言
在计算机编程中,汇编语言(Assembly Language)是一种低级编程语言,语言使用的指令与具体平台紧密相关。这意味着,针对不同 CPU 体系架构设计的汇编语言无法共用,也不具备可移植性。汇编代码可以经由汇编程序(如 as)进行转换,从而得到二进制的可执行代码。不同于高级编程语言,汇编语言在机器指令之上基本不具有任何抽象。因此,通过观察一个程序的汇编代码,我们可以详细了解到程序运行时的每一个具体步骤。
指令集中的寄存器
寄存器有时也被称为“寄存器文件(Register File)”,你可以把它简单理解为由 CPU 提供的一组位于芯片上的高速存储器硬件,可用于存储数据。通常来说,寄存器可以使用 SRAM 来实现。SRAM 是一种高速随机访问存储器,它将每个位的数据存放在一个对应的“双稳态”存储器中,从而保持较强的抗干扰能力和较快的数据访问速度。在整个计算机体系架构中,寄存器拥有最快的数据访问速度和最低的延迟。
通常来说,我们在汇编代码中使用的寄存器可能并不与 CPU 上的物理寄存器完全一一对应,CPU 会使用额外的方式来保证它们之间的动态对应关系。这些参与到程序运行过程的寄存器,一般可以分为:通用目的寄存器、状态寄存器、系统寄存器,以及用于支持浮点数计算和 SIMD 的 AVX、SSE 寄存器等。
在这些寄存器中,通用目的寄存器一般用于存放程序运行过程中产生的临时数据,这些寄存器在大多数情况下都可以被当作普通寄存器使用。而在某些特殊情况下,它们可能会被用于存放指令计算结果、系统调用号,以及与栈帧相关的内存地址等信息。状态寄存器一般用于存放与指令执行结果相关的状态信息,比如指令执行是否引起进位、计算结果是否为 0 等。系统寄存器一般由操作系统使用,这些寄存器描述了与虚拟内存、中断、CPU 模式等有关的信息。
在 x86-64 架构下,CPU 指令集架构(ISA)中一共定义了 16 个通用目的寄存器,这些寄存器最大可以存放 4 个字,即 64 位长的数据。在汇编代码中,我们可以使用每个寄存器不同部分对应的别名,来针对性地访问它们的低 8 位、低 16 位、低 32 位,以及完整的 64 位数据。关于这些寄存器的具体名称,你可以参考下面这张图:
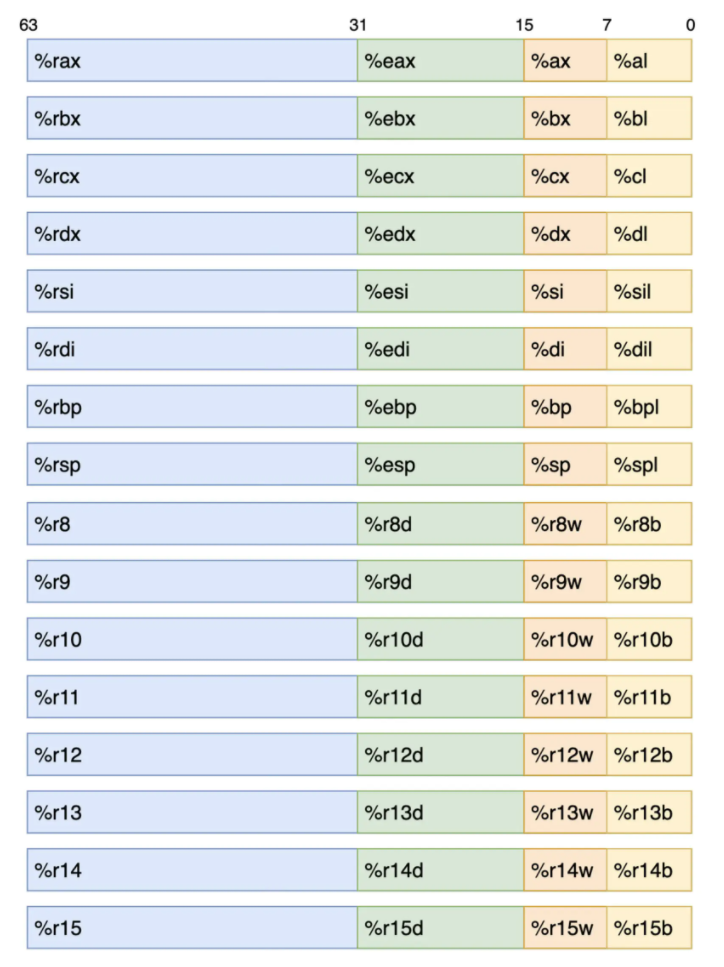
这张图怎么看呢?这里以我们之前遇到的 ebx 寄存器为例:观察上图可以得知,通过 ebx,我们可以访问大小为 32 位的数据,该数据为寄存器 rbx 的低 32 位。因此,直接使用 rbx 便可访问该寄存器的全部 64 位数据。而使用 bx 与 bl ,便可相应访问该寄存器的低 16 位与低 8 位数据。
另外,还需注意的一点是:我们可以通过不同的寄存器别名来读写同一寄存器不同位置上的数据。当某个指令需要重写寄存器的低 16 位或低 8 位数据时,寄存器中其他位上的数据不会被修改。而当指令需要重写寄存器低 32 位的数据时,高 32 位的数据会被同时复位,即置零。
数据的存储形式
对于大多数计算机而言,通常其内部会使用补码(Two’s-complement)的格式来存放有符号整数,使用直接对应的二进制位格式来存放无符号整数,使用 IEEE-754 标准编码格式来存放浮点数,也就是小数。实际上,计算机在看待数据时,并不会区分其符号性,而符号性的差异仅体现在计算机指令操作数据时的具体使用方式上。
补码
使用补码来存放有符号整数的一个优点是,CPU 在针对有符号数进行加减法计算时,不需要由于加数的符号性不同而采用多个底层加法电路,这样便可减轻电路设计的负担,另一方面也可以降低 CPU 的物理尺寸。
一个补码所表示的实际数值,由其负权重位的值与正权重位的值求和而来,其中负权重位对应于最高有效位(MSB)的符号位,即该位的二进制值在计算时按负值累加。其余各位一起对应正权重位,即这些位对应的二进制值在计算时按正值累加。那具体该怎样计算呢?我们来看一个简单的例子。
假设我们有一组补码 “1101”,那么应该如何得到它对应的有符号整数值呢?按照顺序,我们首先计算得到该补码对应负权重位的值为 -8,而正权重位的值为 5,因此该补码对应的实际值为 -3(-8+5)。具体计算步骤可以参考下图(图中的 B2T 表示 “Binary to Two’s-complement”,即“二进制转补码”):
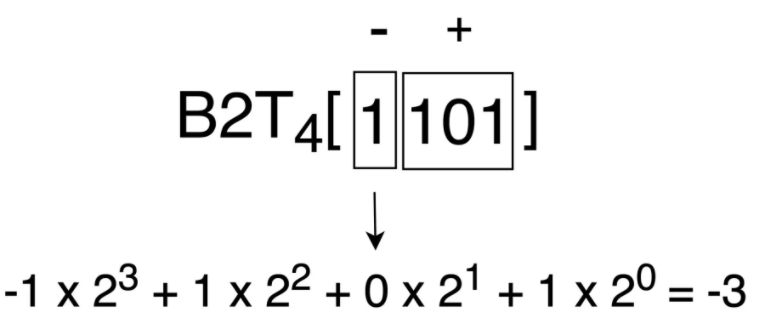
在计算负权重位时,其权重应取负值,正权重位取正值。通过上面的计算过程,你可以清楚地看到,对于一个 4 位补码,它可以表示的最大值与最小值分别是多少。计算最大值时,符号位置 0,其他位均置 1,可以得到能表示的最大值 7。计算最小值时,符号位置 1,其他位均置 0,可以得到最小值 -8。负整数的值可表示范围比正整数多 1 个,这也是所有有符号整数的一个重要特征。
首先,我们来计算一下有符号整数 3 对应的四位补码,可以得到一个二进制序列 “0011”。将该二进制序列与上述 -3 对应的二进制序列1101相加,通过进位可以得到序列 “10000”,该序列可以表示无符号正整数 16。
因此,我们可以得到这样一个结论:对于非负数 x,我们可以用 2w−x 来计算 −x 的 w 位表示。套用在上述的例子中,可以得到“在四位补码的情况下,对于非负数 3,可以用无符号数 13 (即 16−3) 的位模式来表示有符号数 -3 的位模式”这个结论,即两者位模式相同。而补码的英文名称正是对 x、−x 和 2w 三者之间的关系进行的总结。
所以,补码的英文名称是 Two’s-complement ,可直译为“对数字 2 的补充”。
IEEE-754
IEEE-754 是一个被众多硬件浮点计算单元(FPU)采用的浮点数标准,这个标准解决了浮点数在硬件实现上的很多问题,使其更具可移植性。对于 IEEE-754,一个值得介绍的特点是它对浮点数的存储格式设计,使得计算机可以简单地使用对于整数的排序函数,来对浮点数进行排序。
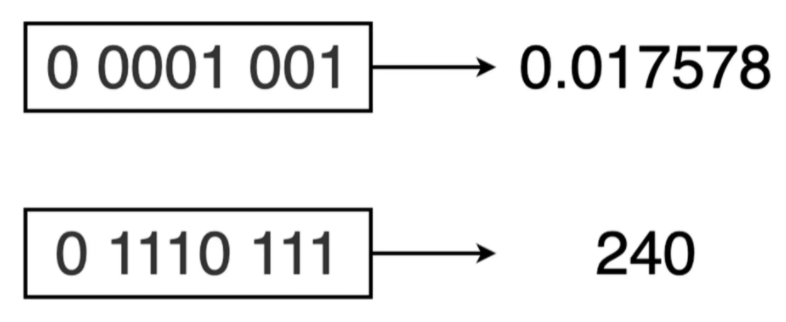
举个例子,对于无符号数的二进制序列来说,0010 的值肯定要小于1000 (2 < 8)。这对计算机来说很好判断。而对基于 IEEE-754 编码的 8 位浮点数(4 位阶码位,3 位小数位)二进制序列 0 0001 001 和 0 1110 111 来说,判断其大小也同样十分简单。除去最左侧的符号位外,直接将其余各位当作无符号整数序列值进行比较,所得结果同样适用于对应的浮点数序列。
图灵机
大名鼎鼎的阿兰·图灵。在他的众多贡献中,很重要的一个就是提出了一种理想中的机器:图灵机。图灵机是一个抽象的模型,它是这样的:有一条无限长的纸带,纸带上有无限个小格子,小格子中写有相关的信息,纸带上有一个读头,读头能根据纸带小格子里的信息做相关的操作并能来回移动。用图灵机执行一下“1+1=2”的计算,我们定义读头读到“+”之后,就依次移动读头两次并读取格子中的数据,最后读头计算把结果写入第二个数据的下一个格子里,整个过程如下图:
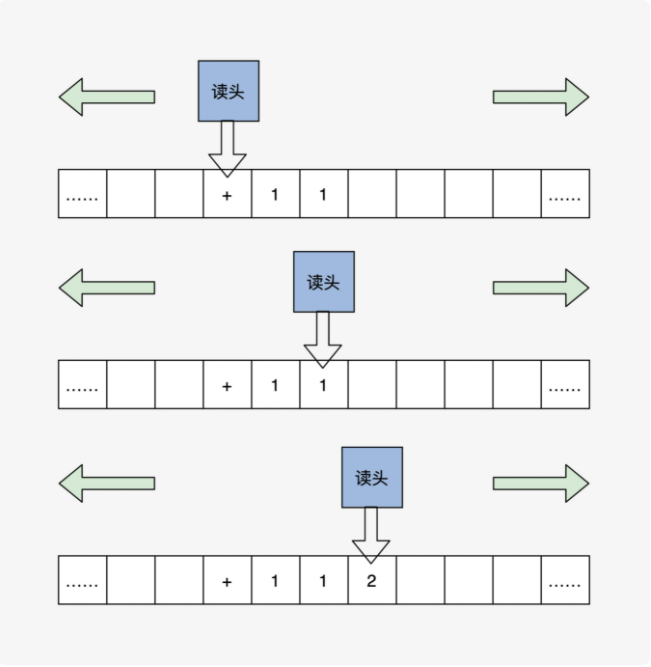
这个理想的模型是好,但是理想终归是理想,想要成为现实,我们得想其它办法。
冯诺依曼体系结构
冯诺依曼提出了电子计算机使用二进制数制系统和储存程序,并按照程序顺序执行。
根据冯诺依曼体系结构构成的计算机,必须具有如下功能:
- 把程序和数据装入到计算机中;
- 必须具有长期记住程序、数据的中间结果及最终运算结果;
- 完成各种算术、逻辑运算和数据传送等数据加工处理;
- 根据需要控制程序走向,并能根据指令控制机器的各部件协调操作;
- 能够按照要求将处理的数据结果显示给用户。
为了完成上述的功能,计算机必须具备五大基本组成部件:
- 装载数据和程序的输入设备;
- 记住程序和数据的存储器;
- 完成数据加工处理的运算器;
- 控制程序执行的控制器;
- 显示处理结果的输出设备。
根据冯诺依曼的理论,我们只要把图灵机的几个部件换成电子设备,就可以变成一个最小核心的电子计算机,如下图:
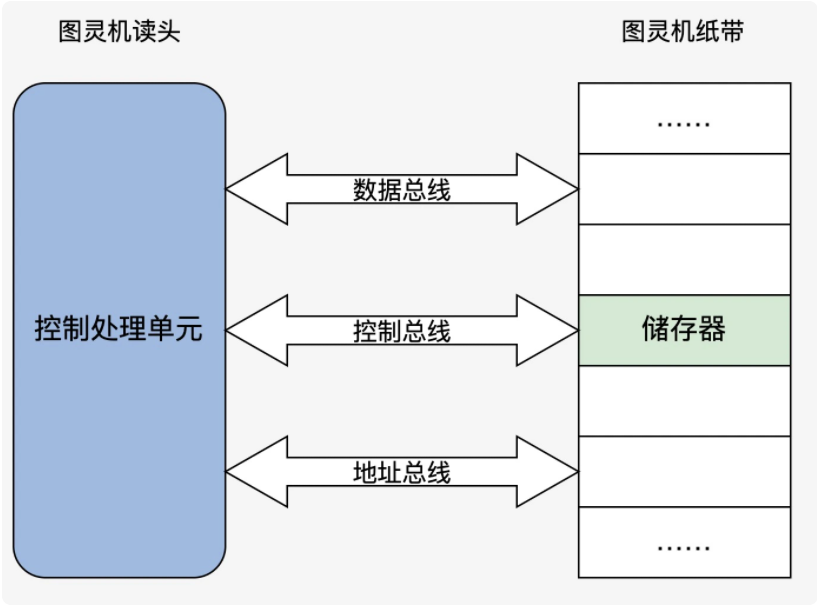
是不是非常简单?这次我们发现读头不再来回移动了,而是靠地址总线寻找对应的“纸带格子”。读取写入数据由数据总线完成,而动作的控制就是控制总线的职责了。
计算机屏幕
计算机屏幕显示往往是显卡的输出,显卡有很多形式:集成在主板的叫集显,做在 CPU 芯片内的叫核显,独立存在通过 PCIE 接口连接的叫独显,性能依次上升,价格也是。我们要在屏幕上显示字符,就要编程操作显卡。
其实无论我们 PC 上是什么显卡,它们都支持一种叫 VESA 的标准,这种标准下有两种工作模式:字符模式和图形模式。显卡们为了兼容这种标准,不得不自己提供一种叫 VGABIOS 的固件程序。
下面,我们来看看显卡的字符模式的工作细节。它把屏幕分成 24 行,每行 80 个字符,把这(24*80)个位置映射到以 0xb8000 地址开始的内存中,每两个字节对应一个字符,其中一个字节是字符的 ASCII 码,另一个字节为字符的颜色值。如下图所示:
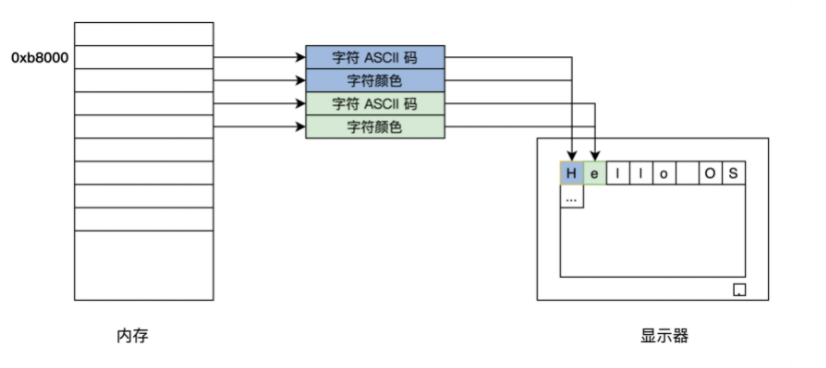
明白了显卡的字符模式的工作细节,我们就可以编写自己的printf函数了,代码如下:
void _strwrite(char* string)
{
char* p_strdst = (char*)(0xb8000);//指向显存的开始地址
while (*string)
{
*p_strdst = *string++;
p_strdst += 2;
}
return;
}
void printf(char* fmt, ...)
{
_strwrite(fmt);
return;
}代码很简单,printf 函数直接调用了 _strwrite 函数,而 _strwrite 函数正是将字符串里每个字符依次定入到 0xb8000 地址开始的显存中,而 p_strdst 每次加 2,这也是为了跳过字符的颜色信息的空间。



